Kennzahlen der nationalen F&E-Systeme
Forschungsausgaben
Die Höhe der Ausgaben für Forschung und Entwicklung ist eine zentrale Kenngröße für den Stellenwert, welchen ein Land seinem Wissenschaftssektor einräumt.
Anteil der gesamten Ausgaben für Forschung und Entwicklung am Bruttoinlandsprodukt der EU-28 Staaten (Mittelwert der Jahre 2014-2019):

Die Governmental Budget Allocation on Research and Development (GBARD) gibt Aufschluss über die staatlichen Ressourcen, die für den Wissenschaftssektor bereitgestellt werden. Die Karte stellt die GBARD pro Kopf dar (Mittelwert der Jahre 2014-2020, logarithmisierte Darstellung):

Anteil der gesamten Ausgaben für Forschung und Entwicklung am BIP sowie der Anteil des GBARD am BIP als Mittelwert der Jahre 2014-2019:
Ausgaben für den Forschung und Entwicklung der Jahre 2014-2019 geordnet nach dem Anteil am BIP:
| Nr. | Land | Anteil BIP für F&E | GBARD pro Kopf |
|---|---|---|---|
| 1 | Schweden | 3,25 % | 365,07 € |
| 2 | Österreich | 3,10 % | 326,78 € |
| 3 | Dänemark | 3,03 % | 466,72 € |
| 4 | Deutschland | 2,99 % | 357,45 € |
| 5 | Finnland | 2,85 % | 354,73 € |
| 6 | Belgien | 2,53 % | 251,62 € |
| 7 | Frankreich | 2,23 % | 209,78 € |
| 8 | Slowenien | 2,08 % | 85,92 € |
| 9 | Niederlande | 2,02 % | 301,03 € |
| 10 | Tschechien | 1,86 % | 108,83 € |
| 11 | Vereinigtes Königreich | 1,67 % | 200,25 € |
| 12 | Italien | 1,37 % | 146,28 € |
| 13 | Estland | 1,36 % | 117,40 € |
| 14 | Ungarn | 1,35 % | 39,02 € |
| 15 | Portugal | 1,30 % | 68,52 € |
| 16 | Luxemburg | 1,27 % | 600,38 € |
| 17 | Irland | 1,22 % | 157,15 € |
| 18 | Spanien | 1,22 % | 131,02 € |
| 19 | Polen | 1,03 % | 45,63 € |
| 20 | Griechenland | 1,02 % | 91,77 € |
| 21 | Litauen | 0,95 % | 45,90 € |
| 22 | Slowakei | 0,91 % | 58,82 € |
| 23 | Lettland | 0,58 % | 28,17 € |
| 24 | Rumänien | 0,47 % | 19,82 € |
Wissenschaftler in den EU-Staaten
Neben den Forschungsausgaben ist auch die Zahl der Menschen, die forschend im Wissenschaftssektor eines Landes tätig sind, von großer Bedeutung für die Stärke dieses Sektors. Unterschieden wird in den Daten zwischen allen Menschen im F&E-Bereich und Wissenschaftlern, die in Regierungseinrichtungen (Universitäten, Akademien, Forschungszentren etc.) angestellt sind.
Anteil der Wissenschaftler an der Gesamtbevölkerung der Länder (Mittelwert der Jahre 2014-2018, nur OECD-Staaten):

Anteil der Wissenschaftler an der Bevölkerung sowie der Anteil der Regierungswissenschaftler an den Wissenschaftlern (Mittelwert der Jahre 2014-2018, nur OECD-Staaten):
Gesamtzahl der Wissenschaftler und ihr Anteil an der Bevölkerung sowie Gesamtzahl der Regierungswissenschaftler und deren Anteil an der Gesamtzahl der Wissenschaftler, Mittelwerte der Jahre 2014-2018 (nur OECD-Staaten):
| Nr. | Land | Wiss. (gesamt) | Anteil | Regierungswiss. | Anteil |
|---|---|---|---|---|---|
| 1 | Deutschland | 604.578 | 0,73 | 63.539 | 10,51 |
| 2 | Vereinigtes Königreich | 510.705 | 0,76 | 8.418 | 1,65 |
| 3 | Frankreich | 393.925 | 0,59 | 29.654 | 7,53 |
| 4 | Spanien | 220.760 | 0,47 | 33.263 | 15,07 |
| 5 | Italien | 187.310 | 0,31 | 29.624 | 15,82 |
| 6 | Polen | 149.431 | 0,39 | 9.275 | 6,21 |
| 7 | Niederlande | 113.629 | 0,66 | 12.102 | 10,65 |
| 8 | Schweden | 107.902 | 1,05 | 12.806 | 11,87 |
| 9 | Portugal | 86.261 | 0,84 | 4.914 | 5,70 |
| 10 | Österreich | 80.850 | 0,91 | 5.173 | 6,40 |
| 11 | Belgien | 76.288 | 0,66 | 4.674 | 6,13 |
| 12 | Griechenland | 61.176 | 0,57 | 15.873 | 25,95 |
| 13 | Dänemark | 60.493 | 1,04 | 2.549 | 4,21 |
| 14 | Finnland | 54.910 | 0,99 | 4.774 | 8,69 |
| 15 | Tschechien | 57.806 | 0,54 | 10.131 | 17,53 |
| 16 | Ungarn | 42.844 | 0,44 | 6.543 | 15,27 |
| 17 | Irland | 33.954 | 0,69 | 592 | 1,74 |
| 18 | Rumänien | 27.485 | 0,14 | 6.959 | 25,32 |
| 19 | Slowakei | 26.362 | 0,48 | 4.278 | 16,23 |
| 20 | Litauen | 18.475 | 0,66 | 2.405 | 13,02 |
| 21 | Slowenien | 12.842 | 0,61 | 2.083 | 16,22 |
| 22 | Lettland | 7.622 | 0,40 | 910 | 11,94 |
| 23 | Estland | 7.274 | 0,55 | 649 | 8,92 |
| 24 | Luxemburg | 3.373 | 0,54 | 680 | 20,16 |
Veröffentlichungen
Die Zahl der wissenschaftlichen Veröffentlichungen pro Jahr stellt einen Richtwert für die Forschungstätigkeit der Wissenschaftler eines Landes dar. Besonders häufig zitierte Veröffentlichungen (Top 10-Paper) können als Indikator für die wissenschaftliche Exzellenz und den Impact von Wissenschaftlern gesehen werden.
Anteil der Top 10-Paper an allen Veröffentlichungen eines Landes:
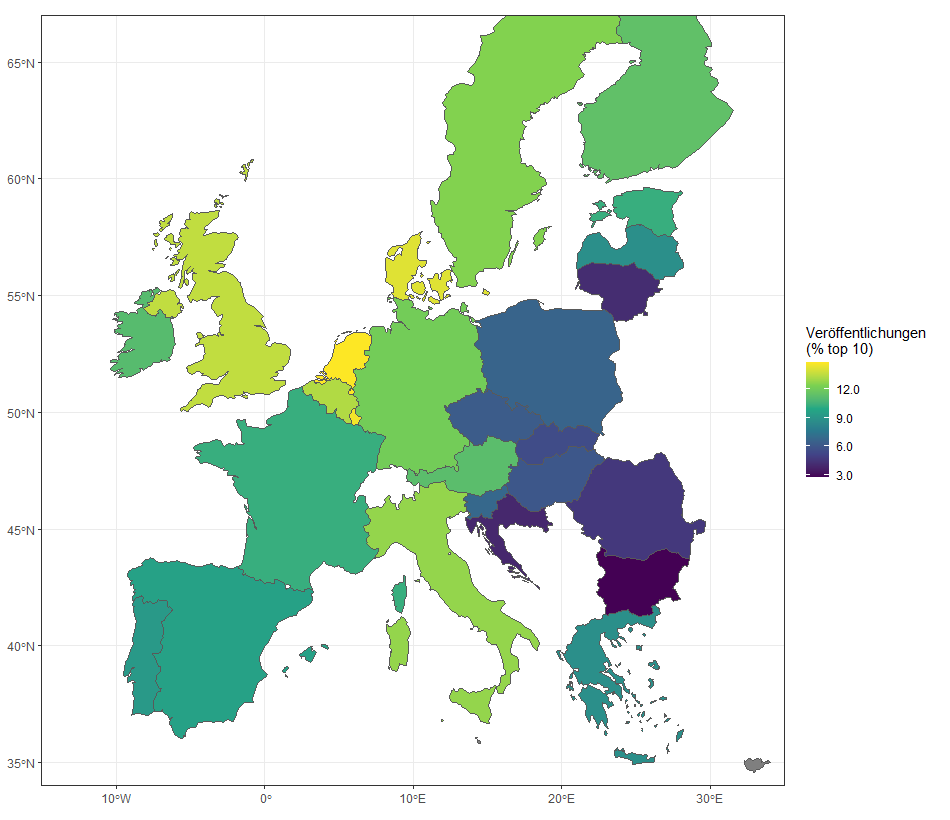
Die Grafik zeigt die Anzahl an Veröffentlichungen im Jahr 2015 mit ihrem Anteil an Top 10-Paper. Mit Klicken auf die Legende lassen sich einzelne Elemente an- und abschalten:
Gerundete Gesamtzahl der Paper sowie Top 10-Paper und deren Anteil an der Gesamtzahl für das Jahr 2015, absteigend sortiert nach Gesamtzahl:
| Nr. | Land | Paper | Top 10 | Anteil Top 10 |
|---|---|---|---|---|
| 1 | Vereinigtes Königreich | 124.000 | 16.823 | 13.6 % |
| 2 | Deutschland | 113.000 | 13.593 | 12.1 % |
| 3 | Italien | 78.000 | 9.925 | 12.8 % |
| 4 | Frankreich | 77.000 | 7.920 | 10.3 % |
| 5 | Spanien | 62.000 | 5.946 | 9.6 % |
| 6 | Niederlande | 35.000 | 5.177 | 14.8 % |
| 7 | Polen | 33.000 | 2.164 | 6.6 % |
| 8 | Schweden | 23.000 | 2.859 | 12.5 % |
| 9 | Belgien | 19.000 | 2.483 | 13.3 % |
| 10 | Tschechien | 17.000 | 1.043 | 6.2 % |
| 11 | Portugal | 16.000 | 1.495 | 9.2 % |
| 12 | Dänemark | 16.000 | 2.190 | 14.2 % |
| 13 | Österreich | 14.000 | 1.574 | 11.2 % |
| 14 | Griechenland | 13.000 | 1.096 | 8.7 % |
| 15 | Finnland | 12.000 | 1.399 | 11.4 % |
| 16 | Rumänien | 11.000 | 524 | 4.6 % |
| 17 | Irland | 8.000 | 886 | 11.1 % |
| 18 | Ungarn | 7.000 | 402 | 6 % |
| 19 | Slowakei | 5.000 | 283 | 5.5 % |
| 20 | Kroatien | 5.000 | 175 | 3.9 % |
| 21 | Slowenien | 4.000 | 274 | 6.8 % |
| 22 | Litauen | 3.000 | 103 | 4.1 % |
| 23 | Bulgarien | 3.000 | 70 | 2.7 % |
| 24 | Lettland | 2.000 | 130 | 8.7 % |
| 25 | Estland | 2.000 | 186 | 10.3 % |
| 26 | Luxemburg | 1.000 | 130 | 14.6 % |
Triadische Patentfamilien
Die Zahl der triatischen Patentfamilien kann als Indikator für die Innovationsstärke eines Wirtschaftsstandortes herangezogen werden. Ein triadisches Patent liegt vor, wenn es für eine Erfindung sowohl beim Europäischen Patentamt, beim United States Patent and Trademark Office und beim Japan Patent Office gewährt wurde.
Anzahl der triadischen Patente pro Wissenschaftler (Mittelwert der Jahre 2014-2018, nur OECD-Staaten):
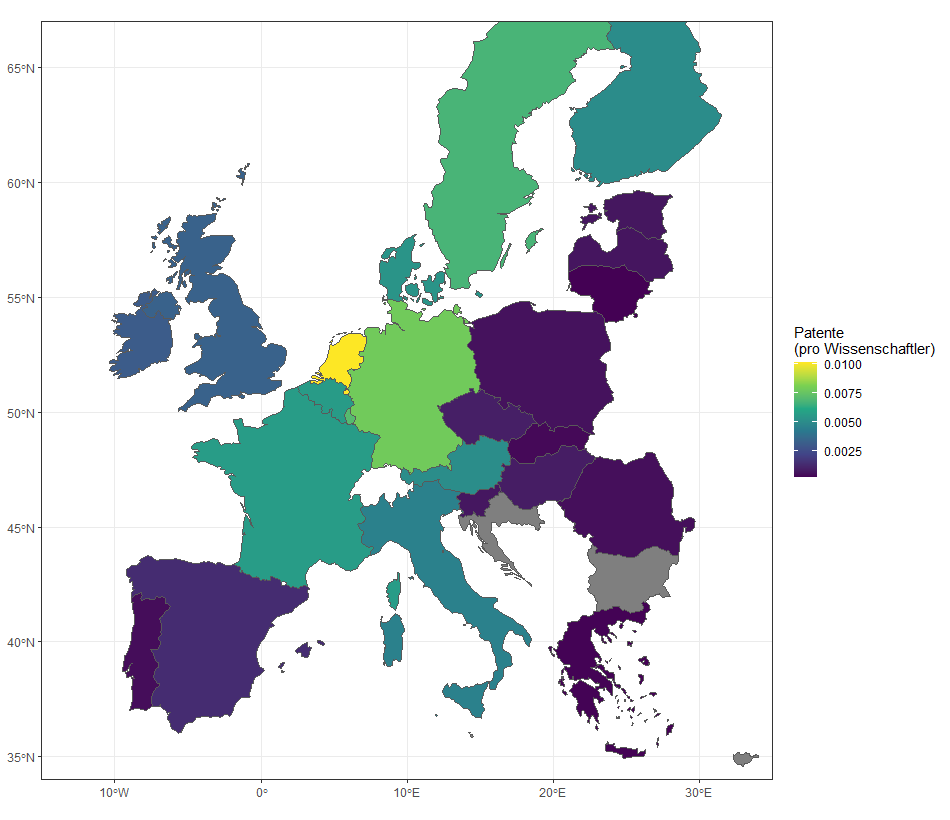
Anzahl der triadischen Patente pro Wissenschaftler als Mittelwert der Jahre 2014-2018 (nur OECD-Staaten):
Anzahl der triatischen Patente sowie der triatischen Patente pro Wissenschaftler als Mittelwert der Jahre 2014-2018, absteigend sortiert nach Patentzahl (nur OECD-Staaten):
| Nr. | Land | Triadische Patente | Patente pro Wiss. |
|---|---|---|---|
| 1 | Deutschland | 4.707,00 | 0,00779 |
| 2 | Frankreich | 2.226,24 | 0,00565 |
| 3 | Vereinigtes Königreich | 1.678,76 | 0,00329 |
| 4 | Niederlande | 1.145,59 | 0,01008 |
| 5 | Italien | 846,11 | 0,00452 |
| 6 | Schweden | 724,22 | 0,00671 |
| 7 | Belgien | 428,01 | 0,00561 |
| 8 | Österreich | 406,59 | 0,00503 |
| 9 | Dänemark | 321,98 | 0,00532 |
| 10 | Spanien | 291,28 | 0,00132 |
| 11 | Finnland | 273,69 | 0,00498 |
| 12 | Irland | 103,98 | 0,00306 |
| 13 | Polen | 80,42 | 0,00054 |
| 14 | Tschechien | 51,12 | 0,00088 |
| 15 | Portugal | 37,04 | 0,00043 |
| 16 | Ungarn | 34,92 | 0,00082 |
| 17 | Luxemburg | 23,66 | 0,00701 |
| 18 | Griechenland | 13,99 | 0,00023 |
| 19 | Rumänien | 12,81 | 0,00047 |
| 20 | Slowakei | 9,27 | 0,00035 |
| 21 | Slowenien | 8,40 | 0,00065 |
| 22 | Estland | 4,70 | 0,00065 |
| 23 | Lettland | 4,67 | 0,00061 |
| 24 | Litauen | 3,43 | 0,00019 |
Scientific Development Index
Der Scientific Development Index soll, angelehnt an den Human Development Index, einen Wert für die wissenschaftliche Leistungsfähigkeit eines Landes ermitteln. Berücksichtigt werden dabei die inputorientierten Faktoren Ausgaben eines Landes für Forschung & Entwicklung sowie Anteil der Wissenschaftler an der Gesamtbevölkerung, die outputorientieren Faktoren triadische Patentfamilien pro Wissenschaftler und Anteil der Top-10 Veröffentlichungen unter allen Veröffentlichungen, sowie als Hintergrundfaktor der Human Development Index.
Beim Scientific Development Index handelt es sich um einen kombinierten Index, erstellt aus folgenden Sub-Indizes:
| Berechnung | Erläuterung |
|---|---|
| \[ AI = \frac{(BIP_{FE} - 0.1)}{(5 - 0.1)} \] | Ausgabenindex: Anteil des BIP für Forschung und Entwicklung, mit Schwellenwerten von \([5\%,0.1\%]\). |
| \[ WI = \frac{(WISS_{BEV} - 0.1)}{(1.2 - 0.1)} \] | Wissenschaftlerindex: Anteil der Wissenschaftler an der Gesamtbevölkerung, mit Schwellenwerten von \([1.2\%,0.1\%]\). |
| \[ PI = \frac{(PAT_{WISS} - 0)}{(1 - 0)} \] | Patentindex: Anteil der triadischen Patentfamilien pro Wissenschaftler, mit Schwellenwerten von \([1\%,0\%]\). |
| \[ TI = \frac{(TOP_{10} - 2)}{(20 - 2)} \] | Top-10-Index: Anteil der Top-10 Veröffentlichungen unter allen wissenschaftlichen Veröffentlichungen, mit Schwellenwerten von \([20\%,2\%]\). |
| \[ SDI = \sqrt[3]{HDI \cdot \sqrt[2]{AI \cdot WI} \cdot \sqrt[2]{ PI \cdot TI }} \] | Der Scientific Development Index als geometrischer Mittelwert des HDI sowie des geometrischen Mittelwertes von jeweils AI und WI sowie PI und TI. |
Scientific Development Index, basierend auf den Mittelwerten der Jahre 2014-2019 (nur OECD-Staaten):

SDI, basierend auf den Mittelwerten der Jahre 2014-2019 (nur OECD-Staaten):
Der Scientific Development Index und seine Komponenten, basierend auf den Mittelwerten der Jahre 2014-2019, absteigend sortiert nach SDI (nur OECD-Staaten):
| Nr. | Land | AI | WI | PI | TI | SDI |
|---|---|---|---|---|---|---|
| 1 | Schweden | 0.643 | 0.864 | 0.671 | 0.583 | 0.76 |
| 2 | Dänemark | 0.598 | 0.855 | 0.532 | 0.678 | 0.738 |
| 3 | Deutschland | 0.59 | 0.573 | 0.779 | 0.561 | 0.713 |
| 4 | Niederlande | 0.392 | 0.509 | 1 | 0.711 | 0.707 |
| 5 | Finnland | 0.561 | 0.809 | 0.498 | 0.522 | 0.685 |
| 6 | Österreich | 0.612 | 0.736 | 0.503 | 0.511 | 0.679 |
| 7 | Belgien | 0.496 | 0.509 | 0.561 | 0.628 | 0.651 |
| 8 | Frankreich | 0.435 | 0.445 | 0.565 | 0.461 | 0.586 |
| 9 | Luxemburg | 0.239 | 0.4 | 0.701 | 0.7 | 0.582 |
| 10 | Vereinigtes Königreich | 0.32 | 0.6 | 0.329 | 0.644 | 0.572 |
| 11 | Irland | 0.229 | 0.536 | 0.306 | 0.506 | 0.506 |
| 12 | Italien | 0.259 | 0.191 | 0.452 | 0.6 | 0.468 |
| 13 | Spanien | 0.229 | 0.336 | 0.132 | 0.422 | 0.389 |
| 14 | Slowenien | 0.404 | 0.464 | 0.065 | 0.267 | 0.372 |
| 15 | Estland | 0.257 | 0.409 | 0.065 | 0.461 | 0.367 |
| 16 | Tschechien | 0.359 | 0.4 | 0.088 | 0.233 | 0.365 |
| 17 | Portugal | 0.245 | 0.673 | 0.043 | 0.4 | 0.357 |
| 18 | Ungarn | 0.255 | 0.309 | 0.082 | 0.222 | 0.318 |
| 19 | Griechenland | 0.188 | 0.427 | 0.023 | 0.372 | 0.285 |
| 20 | Polen | 0.19 | 0.264 | 0.054 | 0.256 | 0.284 |
| 21 | Lettland | 0.098 | 0.273 | 0.061 | 0.372 | 0.276 |
| 22 | Slowakei | 0.165 | 0.345 | 0.035 | 0.194 | 0.256 |
| 23 | Litauen | 0.173 | 0.509 | 0.019 | 0.117 | 0.23 |
| 24 | Rumänien | 0.076 | 0.036 | 0.047 | 0.144 | 0.152 |